nPro >
Help >
Geothermal borehole field sizing
Sizing of geothermal borehole fields: Calculation and validation
Geothermal probe fields can be sized and calculated with nPro. On this page you learn which calculation methods are used for the simulation in nPro and how they have been validated.
System design: Geothermal boreholes with heat pumps
To exploit the underground thermal potential, various technologies such as heat pumps or heat exchangers can be used. They supply either individual buildings or entire districts via a heat network. In Figure 1, the connection between the heat pump or heat exchanger and the geothermal borehole extracting heat from the ground is illustrated. The dimensions of the borehole are crucial for the calculation of heat yield. The borehole length (H) defines the depth to which the geothermal probe reaches into the ground. The borehole spacing (B) indicates the horizontal distance between two boreholes and it influences the efficiency of heat extraction. The borehole radius (r) is significant as it affects the contact area between the soil and the probe. These probe parameters are central to designing an efficient geothermal borehole system as they significantly influence the extraction of geothermal energy.
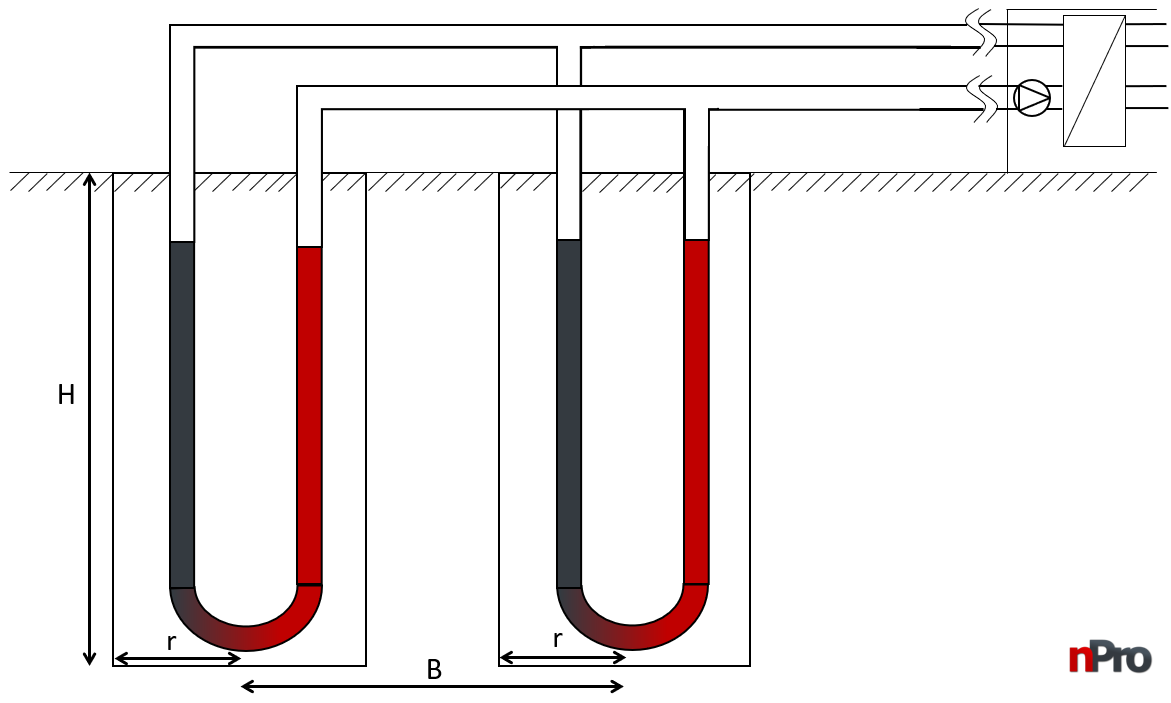
Figure 1: Structure of a geothermal borehole field with heat pump
Methods for geothermal borehole calculation
The calculation basis used in nPro for geothermal borehole fields is based on the work of Prof. Koenigsdorff from the Hochschule Biberach (Germany). It employs models based on the work of the Swedish scientists Eskilson and Hellström, taking into account three load conditions: base load, periodic load, and peak load. The base load represents the average, continuous heat demand throughout the year, while the periodic load reflects monthly fluctuations in heat demand due to seasonal temperature differences. The peak load describes the maximum heat demand in extremely cold periods (coldest hours of the year). Crucial in the calculation is the calculation of fluid temperatures in the probes and their influence on the soil. These calculations are essential to avoid overloading of the geothermal probe field or undesired temperature changes in the ground. Prof. Koenigsdorff has developed the software GEO-HANDlight and validated the results of his calculation methodology with the well-known software Energy Earth Designer (EED) and the German guideline VDI 4640. To determine the thermal resistance of the base load, the g-function introduced by Eskilson is used. This is a thermal step response to heat transfer and considers the interaction between individual boreholes. Different to Koenigsdorff's calculation, nPro uses an open-source simulation core for calculating the g-function, which was developed as part of the doctoral thesis by Massimo Cimmino (today professor at École polytechnique de Montréal in Canada). Detailed information on the calculation basis can be found in the book "Oberflächennahe Geothermie für Gebäude" by Prof. Koenigsdorff, as well as in the user manual for the GEO-HANDlight program (version 5.0). The source code of Prof. Cimmino's open-source computational core is available in the public code repository pygfunction on Github.
How to design a geothermal borehole field with nPro?
The geothermal module in nPro provides 3 essential calculation functions:
-
The calculation of the number of boreholes depending on the specified borehole length, temperature at the heat pump outlet, and borehole spacing.
-
The calculation of the borehole length depending on the borehole arrangement, borehole spacing, and the temperature at the heat pump outlet.
-
The calculation of the temperature at the heat pump outlet depending on a given borehole length, the borehole spacing and the borehole arrangement.
-
The calculation of the temperature profiles at the heat pump outlet depending on the given borehole length, the borehole spacing and the borehole arrangement.
For the borehole calculation, nPro uses the extraction profiles calculated in the operation simulation, the air temperature profile based on the selected location and an assumed peak load duration of 4 hours. A rectangular arrangement of the boreholes is assumed for the calculation.
Validation with EED (Energy Earth Designer)
In the following, the sizing of geothermal probes in nPro will be compared exemplarily with the calculation results from EED (Energy Earth Designer) using two calculation examples. EED is a standard software for geothermal design. For the calculation of the g-function, nPro standardly uses the boundary condition of a uniform borehole wall temperature (UBWT).
Table 1: Fixed input values that do not change in the following validation scenarios (unless specified otherwise).
| Thermal conductivity of soil |
Volumetric heat capacity of soil |
Geothermal heat flux density |
Borehole resistance |
Borehole radius |
Air temperature |
Design period |
| 2.2 W/(mK) |
2.12 MJ/(m³K) |
0.064 W/m² |
0.08 mK/W |
0.081 m |
11.2 °C |
50 years |
Table 2: Load cases for validation scenarios: Regeneration degree describes the ratio of heat introduced into the ground to heat extracted.
| Load case |
Annual heat demand |
Max. monthly heat demand |
Peak heat demand |
Regeneration degree |
| 1 |
351 MWh/year |
57.94 MWh/month |
189 kW |
28.5 % |
| 2 |
287.1 MWh/year |
47.4 MWh/month |
155 kW |
28.6 % |
Table 3: Probe length depending on the probe arrangement, probe spacing (8.65 m or 8 m in load cases 1 and 2), minimum probe entry temperature (-1 °C), temperature difference at probe inlet and outlet (3 K and 3.6 K respectively).
| Load case |
Probe arrangement |
nPro |
EED |
Deviation |
| 1 |
5 x 10 (50 Probes) |
138 m |
140 m |
-1.4 % |
| 2 |
2 x 17 (34 Probes) |
148 m |
140 m |
5.7 % |
The deviations between the calculation results of nPro and EED are small. In the first load case, the probe length deviation is 2 meters (138 meters in nPro instead of 140 meters in EED), and in the second load case, it is 8 meters (148 meters in nPro instead of 140 meters in EED). The relative deviations are 1.4 % in the first load case and 5.7 % in the second load case. These deviations result, among other factors, from the different calculation methods for the g-function. In nPro, the g-function is geometrically calculated using the pygfunction calculation core developed by Massimo Cimmino. Overall, the discrepancies between both software tools are acceptable (approximately 5 - 10 %), especially when considering that the uncertainty of input parameters in the early planning phase of a geothermal system is significantly greater.
Validation with GEO-HANDlight
In addition to the validation with EED, the calculation methodology of nPro was compared to GEO-HANDlight (Version 5.0) by Prof. Koenigsdorff. In this validation, the boundary condition of a uniform heat transfer rate (UHTR) was used to calculate the g-function. In the current version of nPro, on the other hand, the boundary condition of a uniform borehole wall temperature (UBWT) is used by default. This results in slight differences in the calculation of the g-function.
Validation of the borehole length
The following section compares the sizing of geothermal boreholes in nPro with the calculation results from the GEO-HANDlight tool (version 5.0) by Prof. Koenigsdorff.
Definition of validation scenarios
Table 4: Load cases for validation scenarios: The regeneration factor describes the ratio of heat injected into the ground to the heat extracted from the ground.
| Load case |
Annual heat demand |
Max. monthly heat demand |
Peak load heat demand |
Regeneration |
| 1 |
48.74 MWh/a |
12.76 MWh/mon |
41.23 kW |
0 % |
| 2 |
64.66 MWh/a |
9.26 MWh/mon |
54.98 kW |
14.3 % |
| 3 |
36.36 MWh/a |
13.18 MWh/mon |
49.82 kW |
100 % |
Table 5: Fixed input values, which remain unchanged in the subsequent validation scenarios (unless specified otherwise).
| Borehole resistance |
Borehole radius |
Geothermal heat flux density |
Temperature spread probe inlet and outlet |
Location / air temperature |
| 0.1 mK/W |
0.075 m |
0.065 W/m² |
4 K |
Berlin / 10.24 °C |
Validation of the probe length calculation
For various rectangular borehole arrangements, the borehole lengths calculated with nPro and GEO-HANDlight are compared. The deviation results from different methods used to determine the g-function (nPro calculates the g-function geometrically using the the simulation core of Massimo Cimmino, while GEO-HANDlight uses heuristic calculation approaches). Overall, the differences between both tools are insignificant (below 3 % in most cases).
Table 6: Probe length depending on the probe arrangement: For the calculation, the second load case and a heat pump outlet temperature of -5 °C are assumed. The probes are spaced 10 m apart, and the soil has a thermal conductivity of 1.5 W/(mK).
| Probe arrangement |
nPro |
GEO-HANDlight |
Deviation |
| 3x2 |
226 m |
229 m |
-1.3 % |
| 3x3 |
172 m |
186 m |
-7.5 % |
| 6x2 |
136 m |
139 m |
-2.2 % |
| 4x4 |
112 m |
111 m |
0.9 % |
| 6x3 |
99 m |
100 m |
-1 % |
Table 7: Probe length depending on the heat pump outlet temperature: The calculation examines the second load case. The probes are configured in a 4x4 arrangement with a spacing of 10 m. The soil has a thermal conductivity of 1.5 W/(mK).
| Heat pump outlet temperature |
nPro |
GEO-HANDlight |
Deviation |
| -5 °C |
111 m |
111 m |
0 % |
| -3 °C |
129 m |
130 m |
-0.8 % |
| 0 °C |
164 m |
170 m |
-3.5 % |
Table 8: Probe length as a function of probe spacing: The second load case and a heat pump outlet temperature of 0 °C are analysed for the calculation. The probes are placed in a 4x4 arrangement. The ground has a thermal conductivity of 1.5 W/(mK).
| Probe distance |
nPro |
GEO-HANDlight |
Deviation |
| 10 m |
164 m |
170 m |
-3.5 % |
| 15 m |
147 m |
148 m |
-0.7 % |
| 20 m |
137 m |
136 m |
0.7 % |
| 30 m |
124 m |
127 m |
-2.4 % |
| 50 m |
114 m |
119 m |
-4.2 % |
Table 9: Probe length as a function of borehole resistance, borehole radius and thermal conductivity: The second load case and a heat pump outlet temperature of 0 °C are analysed for the calculation. The probes are placed in the 4x4 arrangement with a spacing of 10 m.
| Borehole resistance |
Borehole radius |
Thermal conductivity |
nPro |
GEO-HANDlight |
Deviation |
| 0.08 mK/W |
0.075 m |
1.5 W/(mK) |
158 m |
163 m |
-3.1 % |
| 0.1 mK/W |
0.075 m |
1.5 W/(mK) |
164 m |
170 m |
-3.5 % |
| 0.12 mK/W |
0.075 m |
1.5 W/(mK) |
169 m |
176 m |
-4 % |
| 0.1 mK/W |
0.025 m
| 1.5 W/(mK) |
193 m |
199 m |
-3 % |
| 0.1 mK/W |
0.05 m |
1.5 W/(mK) |
175 m |
181 m |
-3.3 % |
| 0.1 mK/W |
0.1 m |
1.5 W/(mK) |
155 m |
162 m |
-4.3 % |
| 0.1 mK/W |
0.075 m |
2 W/(mK) |
144 m |
146 m |
-1.4 % |
| 0.1 mK/W |
0.075 m |
2.5 W/(mK) |
129 m |
129 m |
0 % |
| 0.1 mK/W |
0.075 m |
3 W/(mK) |
117 m |
117 m |
0 % |
Table 10: Probe length as a function of regeneration: For the calculation, the probes are placed in a 4x4 arrangement with a spacing of 10 m. The ground has a thermal conductivity of 1.5 W/(mK).
| Annual heat extraction |
Regeneration |
nPro |
GEO-HANDlight |
Deviation |
| 48.74 MWh/a |
0 % |
133 m |
134 m |
-0.7 % |
| 64.66 MWh/a |
14.3 % |
164 m |
170 m |
-3.5 % |
| 36.36 MWh/a |
100 % |
85 m |
86 m |
-1.2 % |
Table 11: Probe length as a function of location: The location influences the average air temperature. The second load case and a heat pump outlet temperature of 0 °C are analysed for the calculation. The probes are placed in the 4x4 arrangement with a spacing of 10 m. The ground has a thermal conductivity of 1.5 W/(mK).
| Location |
Mean air temperature |
nPro |
GEO-HANDlight |
Deviation |
| Munich |
9.53 °C |
173 m |
181 m |
-4.4 % |
| Berlin |
10.24 °C |
164 m |
170 m |
-3.5 % |
| Frankfurt |
11.24 °C |
151 m |
155 m |
-2.6 % |
Validation of the calculation of the temperature at the heat pump outlet
To calculate the number of probes, nPro uses the heat pump outlet temperature as a design criterion. Consequently, the heat pump outlet temperature in nPro is compared to that of the GEO-HANDlight tool. A validation of the number of probes is not possible since it cannot be directly determined using the GEO-HANDlight tool.
Table 12: Fixed input values that do not change in the following validation scenarios (unless otherwise specified).
| Borehole resistance |
Borehole radius |
Geothermal heat flux density |
Temperature difference between probe inlet and outlet |
Location / air temperature |
| 0.1 mK/W |
0.075 m |
0.065 W/m² |
4 K |
Berlin / 10.24 °C |
Table 13: Heat pump outlet temperature as a function of the probe arrangement: The second load case and a probe length of 200 m are analysed for the calculation. The probes are 10 m apart and the ground has a thermal conductivity of 2.5 W/(mK).
| Probe arrangement |
nPro |
GEO-HANDlight |
Deviation |
| 3x2 |
-5.2 °C |
-5.5 °C |
0.3 K |
| 3x3 |
-5.9 °C |
-5.9 °C |
0 K |
| 6x2 |
-1.8 °C |
-1.7 °C |
-0.1 K |
| 4x4 |
0.4 °C |
0.7 °C |
-0.3 K |
| 6x3 |
1.6 °C |
2 °C |
-0.4 K |
Table 14: Heat pump outlet temperature as a function of the probe length: The second load case is considered for the calculation. The probes are placed in a 6x3 arrangement with a spacing of 10 m. The ground has a thermal conductivity of 2.5 W/(mK).
| Probe length |
nPro |
GEO-HANDlight |
Deviation |
| 200 m |
4.6 °C |
4.5 °C |
0.1 K |
| 100 m |
-1.4 °C |
-1.1 °C |
-0.3 K |
| 66.67 m |
-5.7 °C |
-5.5 °C |
-0.2 K |
Table 15: Heat pump outlet temperature as a function of the probe spacing: The second load case is considered for the calculation, with a probe length of 200 m. The probes are placed in a 6x3 arrangement. The ground has a thermal conductivity of 2.5 W/(mK).
| Probe distance |
nPro |
GEO-HANDlight |
Deviation |
| 10 m |
-1.4 °C |
-0.4 °C |
-0.3 K |
| 15 m |
-0.4 °C |
-0.3 °C |
-0.1 K |
| 20 m |
0.2 °C |
0.2 °C |
0 K |
| 30 m |
0.8 °C |
0.7 °C |
0.1 K |
| 50 m |
1.4 °C |
1.1 °C |
0.3 K |
Table 16: Heat pump outlet temperature as a function of borehole resistance, borehole radius and thermal conductivity: The second load case and a probe length of 200 m are analysed for the calculation. The probes are placed in the 4x4 arrangement with a spacing of 10 m.
| Borehole resistance |
Borehole radius |
Thermal conductivity |
nPro |
GEO-HANDlight |
Deviation |
| 0.08 mK/W |
0.075 m |
2.5 W/(mK) |
4.6 °C |
4.8 °C |
-0.2 K |
| 0.1 mK/W |
0.075 m |
2.5 W/(mK) |
4.3 °C |
4.5 °C |
-0.2 K |
| 0.12 mK/W |
0.075 m |
2.5 W/(mK) |
4.0 °C |
4.2 °C |
-0.2 K |
| 0.1 mK/W |
0.025 m |
2.5 W/(mK) |
3.2 °C |
3.4 °C |
-0.2 K |
| 0.1 mK/W |
0.05 m |
2.5 W/(mK) |
3.9 °C |
4.1 °C |
-0.2 K |
| 0.1 mK/W |
0.1 m |
2.5 W/(mK) |
4.3 °C |
4.7 °C |
-0.4 K |
| 0.1 mK/W |
0.075 m |
2.5 W/(mK) |
4.3 °C |
4.5 °C |
-0.2 K |
| 0.1 mK/W |
0.075 m |
3 W/(mK) |
4.6 °C |
4.8 °C |
-0.2 K |
| 0.1 mK/W |
0.075 m |
3.5 W/(mK) |
4.9 °C |
5 °C |
-0.1 K |
Table 17: Heat pump outlet temperature as a function of regeneration: For the calculation, the probes are placed in a 6x3 arrangement with a spacing of 10 m. The probes have a length of 200 m and the ground has a thermal conductivity of 2.5 W/(mK).
| Annual heat extraction |
Regeneration |
nPro |
GEO-HANDlight |
Deviation |
| 48.74 MWh/a |
0 % |
1.3 °C |
1.4 °C |
-0.1 K |
| 64.66 MWh/a |
14.3 % |
-1.8 °C |
-1.7 °C |
-0.1 K |
| 36.36 MWh/a |
100 % |
7.8 °C |
7.6 °C |
0.2 K |
Table 18: Heat pump outlet temperature as a function of location: The location influences the average air temperature. The second load case and a probe length of 200 m are analysed for the calculation. The probes are placed in a 6x3 arrangement with a spacing of 10 m.
| Location |
Mean air temperature |
nPro |
GEO-HANDlight |
Deviation |
| Munich |
9.53 °C |
3.6 °C |
3.8 °C |
-0.2 K |
| Berlin |
10.24 °C |
4.3 °C |
4.5 °C |
-0.2 K |
| Frankfurt |
11.24 °C |
5.3 °C |
5.5 °C |
-0.2 K |
Validation with Scientific Study
In addition to the validations with EED and GEO-HANDlight, the calculation results from nPro were compared with those of a scientific study that evaluated 12 software tools for geothermal borehole field sizing, including an intermodel comparison (Ahmadfard et al.: A review of vertical ground heat exchanger sizing tools including an intermodel comparison, Renewable and Sustainable Energy Reviews, 2019) [8]. This validation used a temperature difference condition of 3 K between the inlet and outlet of the borehole to calculate the borehole length. The following compares the dimensioning of geothermal boreholes in nPro with the calculation results from the study.
Table 19: Mean, minimum, and maximum of the calculation results from the 12 examined software tools compared to the calculation results from nPro for the test cases defined in the study (Test 1a to 4).
|
Test 1a |
Test 1b |
Test 2 |
Test 3 |
Test 4 |
| Mean |
60 m |
76 m |
94 m |
100 m |
119 m |
| Minimum |
57 m |
71 m |
91 m |
86 m |
93 m |
| Maximum |
64 m |
81 m |
108 m |
115 m |
129 m |
| nPro |
79 m |
76 m |
99 m |
92 m |
129 m |
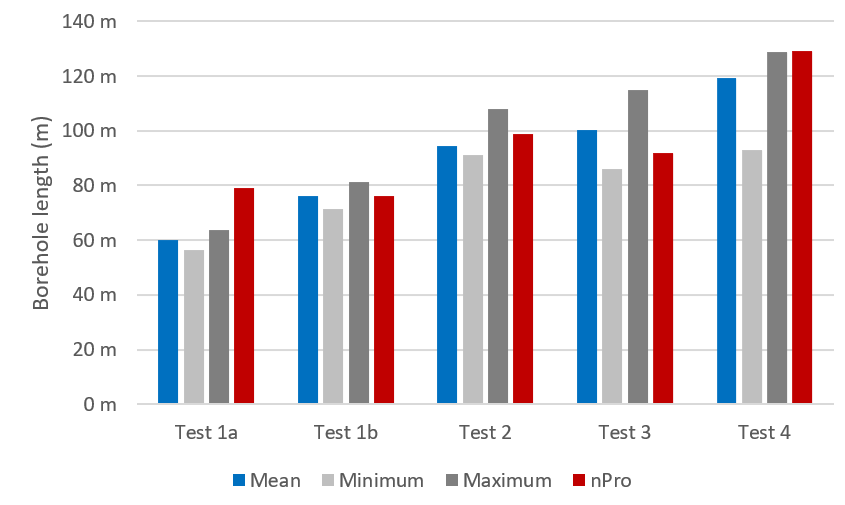
Figure 2: Graphical representation of the validation results: nPro compared to the software tools in the study.
Methodology for determining the probe (borehole) length
To determine the probe length, it is assumed that all probes in the geothermal field are of equal length and hydraulically connected in parallel. The calculation utilizes an iterative approach since the values of the borehole resistance of the base load and the temperature response in the formula to calculate the probe length again depend on the probe length. The iteration continues until the difference between the newly calculated length and the previously calculated length is less than 1 meter. The results of this calculation methodology have been validated with the German guideline VDI 4640 Part 2 in a work by Prof. Koenigsdorff. nPro employs the same calculation approach.
-
Calculation basis:
\begin{gathered}
H= \frac{Q_{Net base load} \cdot (R_{Base load} + R_{B}) + Q_{per} \cdot (R_{per} + R_{B}) + Q_{peak} \cdot (R_{peak} + R_{B})}{\Delta T_{Reaction} \cdot N_{Number of probes}}
\end{gathered}
As an add-on to the Koenigsdorff calculation method, nPro also offers the option of designing the probes under dominant cooling load. If the cooling demand is decisive for the design due to high periodic loads and peak loads (or a low maximum probe outlet temperature) compared to the heat demand, the necessary probe length is designed using the cooling load. In this way, excessively high temperatures at the probe outlet can be avoided.
Calculation of the heat pump outlet temperature
The heat pump outlet temperature corresponds to the temperature of the heat transfer fluid at the probe inlet. Together with the temperature difference across the heat exchanger, it indicates the state of the fluid before and after passing through the probe. The higher the temperature at the probe outlet, the higher the efficiency of the heat pump. The minimum heat pump outlet temperature, which is set in a steady state and is only reached after several decades, is decisive for the design. This steady-state temperature can be determined by the calculation approach.
-
Calculation basis:
\begin{gathered}
T_{HP,out}= T_{Undisturbed soil} + \Delta T_{Base load} + \Delta T_{per} + \Delta T_{peak} - 0.5 \Delta T_{Fluid}
\end{gathered}
Validated value ranges and determination of input values
This section explains which values can be used for the input parameters for the borehole field calculation and from where suitable values can be obtained.
Table 20: Value ranges for which the calculation was validated and possible sources for determining suitable input values.
| Parameter |
Validated area |
Data source |
| Borehole length |
50 - 200 m |
is calculated |
| Borehole spacing |
≥ 6 m |
--- |
| Borehole resistance |
Typical value range: 0.05 - 0.15 (mK)/W |
Thermal Response Test or from analyses, e.g. of geoenergie-konzept.de |
| Borehole radius |
0.025 - 0.1 m |
e.g. overview of geoenergie-konzept.de |
| Thermal conductivity |
1 - 6 W/(mK) |
Thermal Response Test or VDI Guideline 4640 Sheet 1 |
| Geothermal heat flux density |
25 - 135 mW/m² |
Geographical maps, e.g. map on the website of German Geothermal Energy Association
|
Determination of borehole resistance and thermal conductivity
Backfill materials for ground probes can be categorized into conventional and thermally enhanced materials. On average, conventional materials have an increased mean resistance of about 0.1 (mK)/W compared to thermally enhanced materials, which have approximately 0.08 (mK)/W. Additionally, there is an increase in thermal resistance with increasing borehole radius (refer to the overview on geoenergie-konzept.de).
|
Lower limit |
Upper limit |
| Conventional backfilling |
0.075 (mK)/W |
0.15 (mK)/W |
| Thermally improved backfilling |
0.05 (mK)/W |
0.12 (mK)/W |
Table 22: Exemplary values for thermal conductivity and volumetric heat capacity depending on the soil type in accordance with German guideline VDI 4640 sheets 1 and 2.
| Soil type |
Thermal conductivity in W/(mK) |
Volumetric heat capacity
in MJ/(m³K) |
| Clay/silt, water-saturated |
1.8 |
2.0 - 2.8 |
| Sand, moist |
1.4 |
1.3 - 1.6 |
| Sand, water-saturated |
2.4 |
1.3 - 1.6 |
| Gravel/stones, water-saturated |
1.8 |
2.2 - 2.6 |
| Boulder clay/clay |
2.4 |
1.5 - 2.5 |
| Peat, soft lignite |
0.4 |
0.5 - 3.8 |
Sources
-
Koenigsdorff et al.: GEO-HANDlight (Version 5.0) and user manual, 2022: https://innosued.de/energie/geothermie-software-2/
-
Koenigsdorff et al.: "Oberflächennahe Geothermie für Gebäude: Grundlagen und Anwendungen zukunftsfähiger Heizung und Kühlung". Fraunhofer IRB Verlag, 2011. ISBN-13: 978-3816782711.
-
VDI guideline 4640 sheets 1 and 2.
-
Code-Repository pygfunction from Massimo Cimmino
-
Evaluation of borehole resistances of www.geoenergie-konzept.de
-
Koenigsdorff et al.: "GEO-HANDlight - Handrechenverfahren zur überschlägigen Bemessung von Erdwärmesondenfeldern". In: 7. Internationales Anwenderforum Oberflächennahe Geothermie, 25./26. April
2007, Freising. Regensburg: OTTI, 2007, S. 97-101.
-
Koenigsdorff et al.: "Erweiterung des Handrechenverfahrens GEO-HANDlight zur überschlägigen Bemessung von Erdwärmesondenfeldern auf die kombinierte Heizung und Kühlung". In: Der Geothermiekongress 2007, Bochum, 29.-31. Oktober 2007, 2007, S. 82-84.
-
Ahmadfard et al.: A review of vertical ground heat exchanger sizing tools including an intermodel comparison, Renewable and Sustainable Energy Reviews, 2019
This might also interest you



 English
English
 Deutsch
Deutsch


